Равнобедренный треугольник
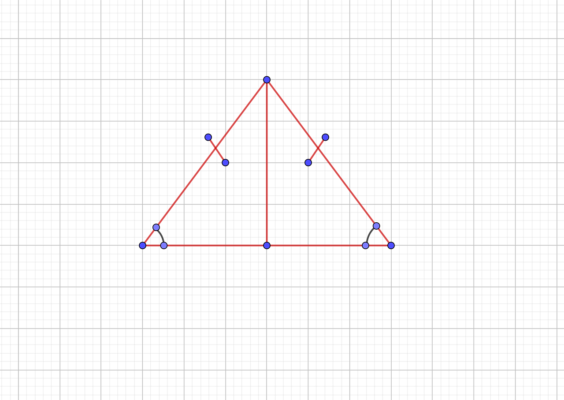
Теорема Вивиани : сумма расстояний от произвольной точки внутри равностороннего треугольника до его сторон постоянна и равна высоте треугольника. В правильном треугольнике окружность девяти точек совпадает со вписанной окружностью. Правильными треугольниками можно замостить плоскость. Стороны этого треугольника параллельны сторонам треугольника Морлея. Если на каждой стороне произвольного треугольника построить по равностороннему треугольнику, то треугольник с вершинами в центрах равносторонних треугольников — тоже равносторонний теорема Наполеона. Правильный сферический треугольник — сферический треугольник с равными сторонами.

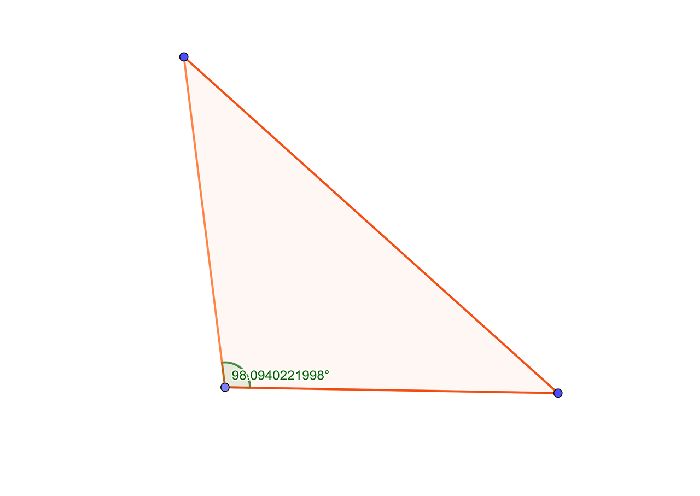


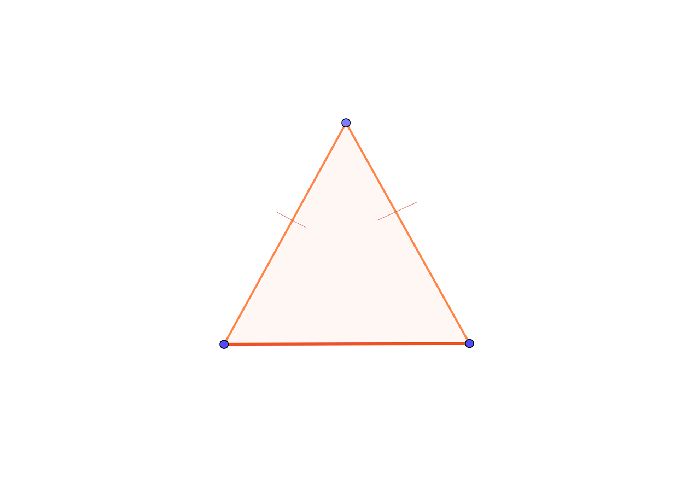


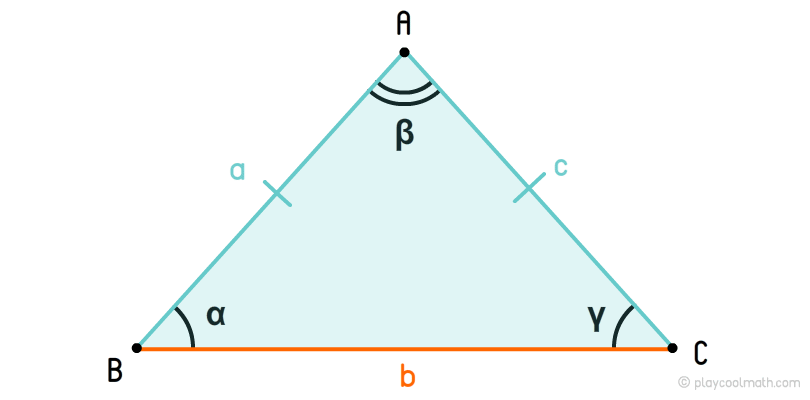
Равнобедренный треугольник: особенности фигуры и его формулы
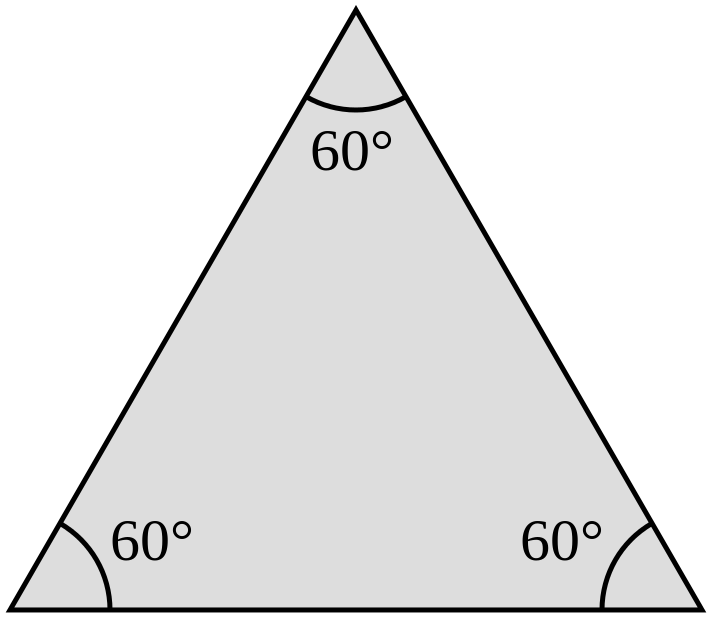
Равнобедренные треугольники хороши тем, что к ним можно применять все правила, которые вышли в статьях ранее, да еще у них и боковые стороны равны, а следовательно и углы при основании. То есть, зная один из углов равнобедренного треугольника, ты можешь найти все три угла. Сказка, а не треугольник! Разберем две разные задачки. В первой нам вообще дан равносторонний треугольник.
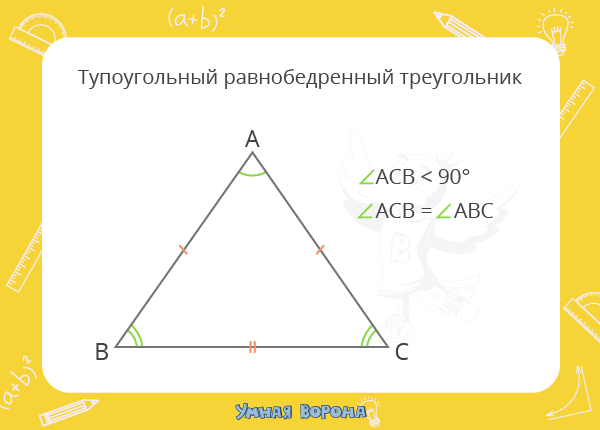


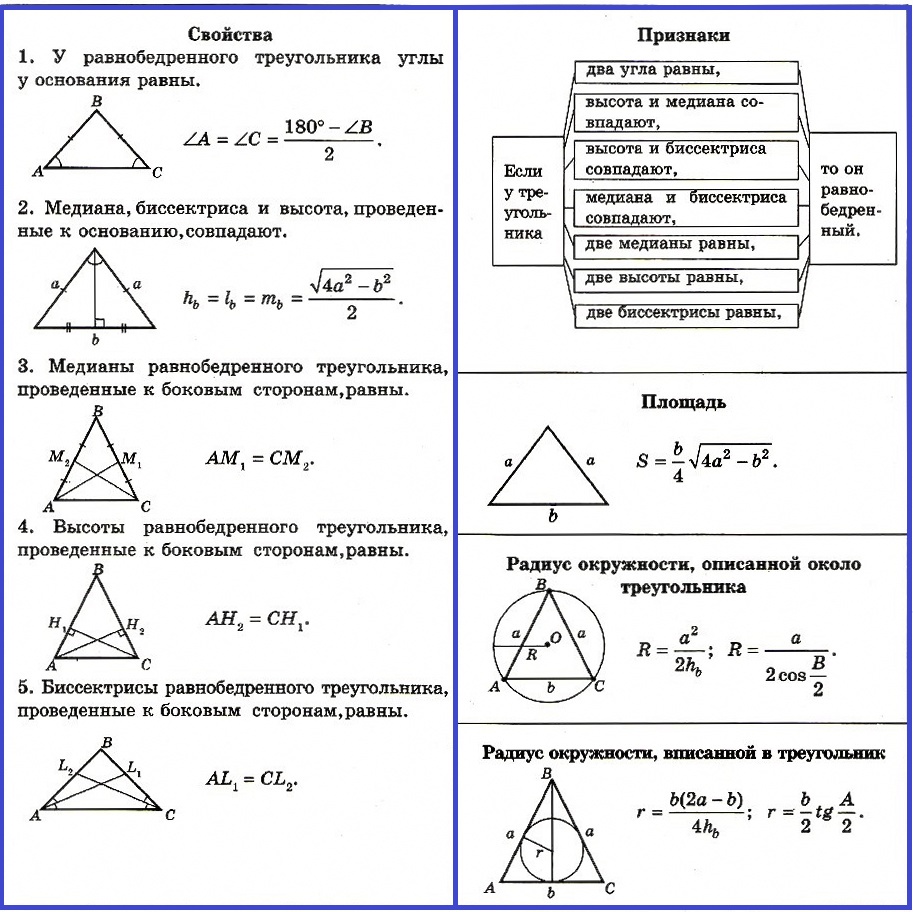


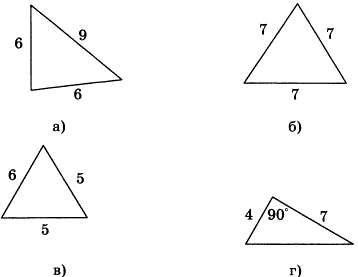
А вот вам такой дурацкий вопрос: может ли равносторонний треугольник быть одновременно прямоугольным? На сфере такой пример вы найдёте без труда, а на плоскости, в евклидовой геометрии? Среди нормальных плоских треугольников, таких, конечно же, нет! Но давайте предположим, что у треугольника все стороны равны 0, он будет явно равносторонним, но в то же самое время, для него тривиальным образом выполняется равенство Пифагора.