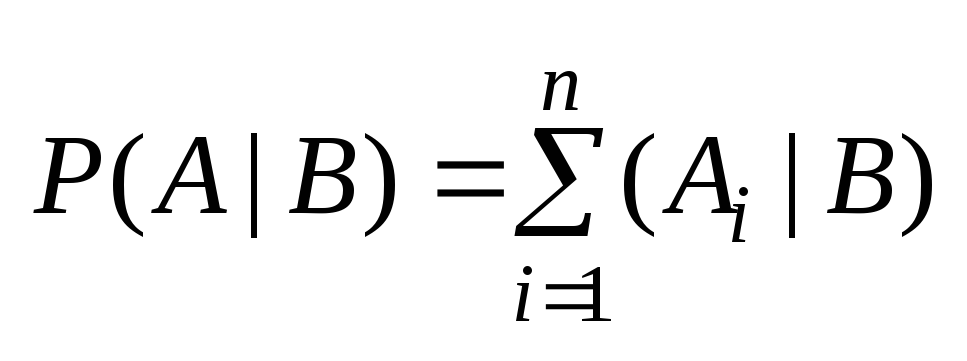
Учебник по теории вероятностей
В теории вероятностей два случайных события называются зависимыми , если наступление одного из них изменяет вероятность наступления другого. Аналогично, две случайные величины называют зависимыми , если значение одной из них влияет на вероятность значений другой. В противных случаях и события, и случайные величины называются независимыми относительно вероятности. Определение 1. Замечание 1. Определение 2.





Высшая математика — просто и доступно! Наш форум, библиотека и блог: mathprofi. Математические формулы, таблицы и другие материалы.



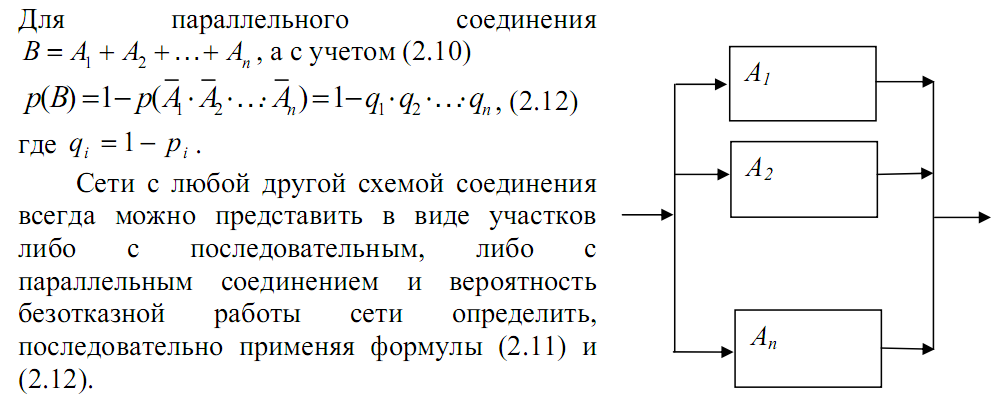






Событие А называется частным случаем события В , если при наступлении А наступает и В. События А и В называются равными, если каждое из них является частным случаем другого. Теорема о сложении вероятностей. Вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий. Произведением событий А и В называется событие АВ , которое наступает тогда и только тогда, когда наступают оба события: А и В одновременно. Случайные события А и B называются совместными , если при данном испытании могут произойти оба эти события.